from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as pltPrincipal Component Analysis ( P.C.A. )
PCA reduces data dimensions by finding key patterns through orthogonal axes (principal components), simplifying complexity while retaining essential information.
Import Libraries
Data
X = np.array([[1, 1], [2, 1], [3, 2], [-1, -1], [-2, -1], [-3, -2]])
plt.plot(X[:, 0], X[:, 1], 'ro')
plt.show()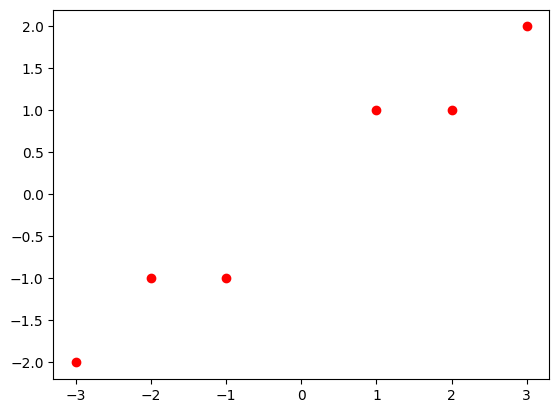
PCA (1 component)
pca = PCA(n_components=1)
pca.fit(X)PCA(n_components=1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
PCA(n_components=1)
sum(pca.explained_variance_ratio_)0.9924428900898052X_transformed = pca.transform(X)
print(X_transformed)[[ 1.38340578]
[ 2.22189802]
[ 3.6053038 ]
[-1.38340578]
[-2.22189802]
[-3.6053038 ]]X_reduced = pca.inverse_transform(X_transformed)
print(X_reduced)
plt.plot(X_reduced[:, 0], X_reduced[:, 1], 'ro')
plt.show()[[ 1.15997501 0.75383654]
[ 1.86304424 1.21074232]
[ 3.02301925 1.96457886]
[-1.15997501 -0.75383654]
[-1.86304424 -1.21074232]
[-3.02301925 -1.96457886]]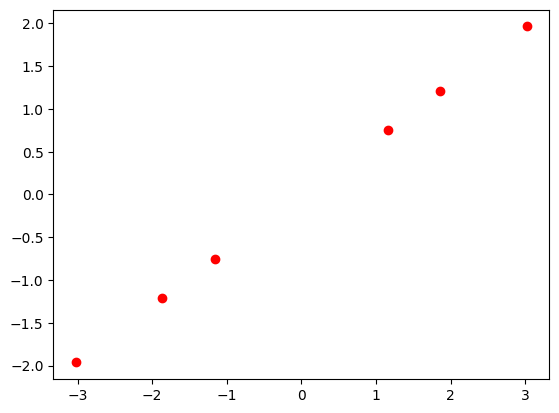
PCA (2 component)
pca = PCA(n_components=2)
pca.fit(X)PCA(n_components=2)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
PCA(n_components=2)
sum(pca.explained_variance_ratio_)1.0X_transformed = pca.transform(X)
print(X_transformed)[[ 1.38340578 0.2935787 ]
[ 2.22189802 -0.25133484]
[ 3.6053038 0.04224385]
[-1.38340578 -0.2935787 ]
[-2.22189802 0.25133484]
[-3.6053038 -0.04224385]]My PCA
def My_PCA(X, k):
X_std = (X - np.mean(X, axis=0))
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
eigenvectors = eig_vecs[:, np.argsort(eig_vals)[::-1]]
pca_mat = eigenvectors[:, :k]
pca = np.dot(X_std, pca_mat)
return pca
print(My_PCA(X, 1))[[ 1.38340578]
[ 2.22189802]
[ 3.6053038 ]
[-1.38340578]
[-2.22189802]
[-3.6053038 ]]