K Means

KMeans is a clustering algorithm that partitions a dataset into K distinct, non-overlapping subsets (clusters) based on similarity patterns within the data. It minimizes the sum of squared distances between data points and their assigned cluster centroids.

Import Libraries

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from mpl_toolkits.mplot3d import Axes3D

KMeans on Dataset

Data

y = load_digits()
x = y.data

print(y.data.shape)
print(y.target.shape)

(1797, 64)
(1797,)

Closest Centroids

def find_closest_centroids(X, centroids):

    idx = np.zeros(X.shape[0], dtype=int)
    distances = np.linalg.norm(X[:, np.newaxis, :]-centroids, axis=-1)
    idx = np.argmin(distances, axis=1)

    return idx

New Centroids

def compute_centroids(X, idx, centroids, k):
    for i in range(k):
        centroids[i] = np.mean(X[idx == i], axis=0)
    return centroids

Cost Fxn

def calculate_cost(X, idx, centroids):
    cost = 0
    for i in range(len(centroids)):
        cluster_points = X[idx == i]
        centroid = centroids[i]
        squared_distances = np.sum((cluster_points - centroid) ** 2)
        cost += squared_distances
    return cost

KMeans

def run_kMeans(X, max_iters, k):
    n, d = X.shape
    centroids = X[np.random.choice(n, k, replace=False)]

    print(f"{'Iteration':<10}{'Cost':<15}")

    prev_cost=np.inf
    cost=0

    for i in range(max_iters):
        if np.abs(prev_cost-cost)<1e-5:
            break
        idx = find_closest_centroids(X, centroids)
        prev_cost=cost
        cost = calculate_cost(X, idx, centroids)

        print(f"{i + 1:<10}{cost:<15}")

        centroids = compute_centroids(X, idx, centroids, k)

    return centroids, idx

Accuracy

a, b = run_kMeans(x, 500, 10)
print("Accuracy =", 100*np.mean(y.target == b) ,"%")

Iteration Cost           
1         2312326.0      
2         1367849.205211381
3         1272514.7623466342
4         1230713.3819844497
5         1217124.8773493604
6         1214638.5685729042
7         1214183.403014829
8         1214039.6629300476
9         1213981.741130655
10        1213950.3799817525
11        1213908.3568474432
12        1213896.1627396639
13        1213875.909452301
14        1213848.8851707997
15        1213820.8739280729
16        1213820.8739280729
Accuracy = 19.47690595436839 %

Image compression with K-means

Original Image

original_img = plt.imread('img.jpg')
plt.imshow(original_img)
plt.show()

# Gives the blue intensity of the pixel at row 50 and column 33.
original_img[50, 33, 2]

3

print("Shape of original_img is:", original_img.shape)

Shape of original_img is: (477, 350, 3)

KMeans

X_img = np.reshape(
    original_img, (original_img.shape[0] * original_img.shape[1], 3))
print("Shape of X_img is:", X_img.shape)

Shape of X_img is: (166950, 3)

max_iter = 30
k = 15
centroids, idx = run_kMeans(X_img, max_iter, k)

Iteration Cost           
1         40518784       
2         49937840       
3         38376899       
4         48464334       
5         38469257       
6         44709319       
7         45348539       
8         48159095       
9         46984087       
10        41761944       
11        45318104       
12        45340223       
13        46252334       
14        47408590       
15        40701877       
16        48466062       
17        52976465       
18        50425878       
19        48800590       
20        49841789       
21        50815087       
22        46825849       
23        47234052       
24        50064839       
25        45833848       
26        44100214       
27        44035480       
28        42271855       
29        46069851       
30        46009134       

RGB Values plot with Centroids

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_img[:, 0], X_img[:, 1], X_img[:, 2], s=0.3)
ax.set_xlabel('R value')
ax.set_ylabel('G value')
ax.set_zlabel('B value')
ax.set_title('RGB Values Plot')
ax.scatter(centroids[:, 0], centroids[:, 1], centroids[:, 2], s=200, alpha=1, marker='*', c='red', zorder=2)
fig.tight_layout()
plt.show()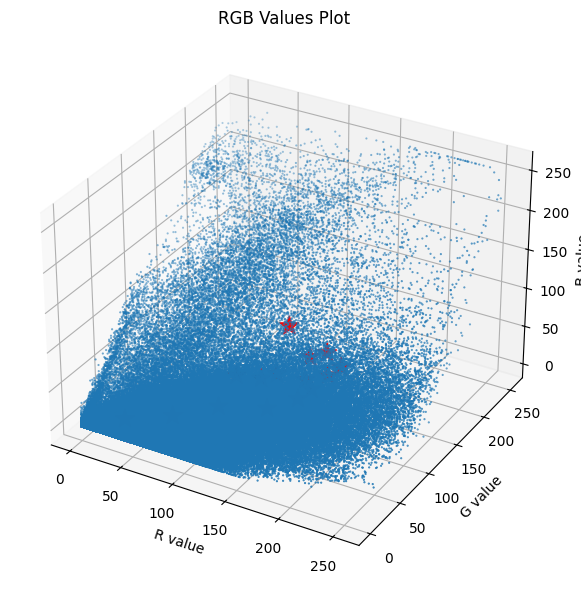

Colors of Centroids

fig, axs = plt.subplots(1, len(centroids))
for i in range(len(centroids)):
    axs[i].imshow(centroids[i].reshape(1, 1, 3))
    axs[i].axis('off')
plt.show()

Decomposed Image

X_recovered = centroids[idx, :]
X_recovered = np.reshape(X_recovered, original_img.shape)

plt.imshow(X_recovered)

plt.show()