Anomaly Detection

Anomaly Detection identifies unusual patterns or outliers in data, crucial for detecting deviations from the norm and highlighting potential irregularities or abnormalities.

Import Libraries

import numpy as np
import matplotlib.pyplot as plt

Dataset

X_train = np.load("data/X_train.npy")
X_test = np.load("data/X_test.npy")
y_test = np.load("data/y_test.npy")

print(X_train.shape)
print(X_test.shape)
print(y_test.shape)

(307, 2)
(307, 2)
(307,)

plt.scatter(X_train[:, 0], X_train[:, 1], marker='x', c='b')

plt.title("The first dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.axis([0, 25, 0, 25])
plt.show()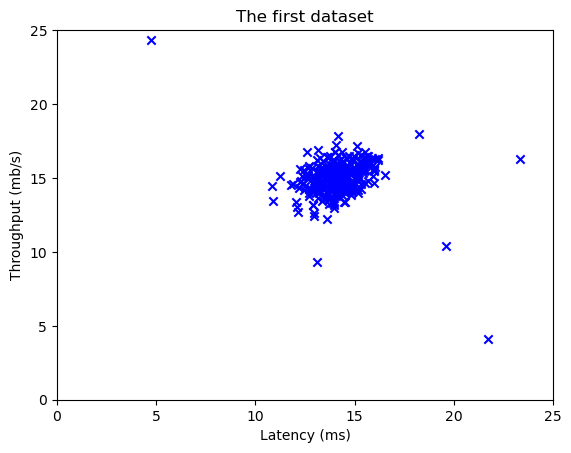

Gaussian Distribution

$$p(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$

$$\text{(Univariate Gaussian Distribution)}$$

$$p(\mathbf{x};\mathit{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{k/2}|\mathbf{\Sigma }{|}^{1/2}}\exp (-\frac{1}{2}(\mathbf{x}-\mathit{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathit{\mu }))$$

$$\mathbf{\Sigma }=\left[\begin{array}{ccccc}{\sigma }_1^2& {\sigma }_{12}& {\sigma }_{13}& \dots & {\sigma }_{1k}\\ {\sigma }_{21}& {\sigma }_2^2& {\sigma }_{23}& \dots & {\sigma }_{2k}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_3^2& \dots & {\sigma }_{3k}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{k1}& {\sigma }_{k2}& {\sigma }_{k3}& \dots & {\sigma }_k^2\end{array}\right]$$

$$\text{(Multivariate Gaussian Distribution)}$$

def estimate_gaussian(X):

    mu = np.mean(X, axis=0)
    var = np.var(X, axis=0)

    return mu, var

def univariate_gaussian(X, mu, var):

    p = (1 / (np.sqrt(2 * np.pi * var))) * np.exp(-((X - mu) ** 2) / (2 * var))

    return p

def multivariate_gaussian(X, mu, var):

    k = len(mu)

    if var.ndim == 1:
        var = np.diag(var)

    X = X - mu
    p = (2 * np.pi)**(-k/2) * np.linalg.det(var)**(-0.5) * \
        np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))

    return p

mu, var = estimate_gaussian(X_train)
print("mu = ", mu)
print("var = ", var)

mu =  [14.11222578 14.99771051]
var =  [1.83263141 1.70974533]

print(univariate_gaussian(X_train[246][0], mu[0], var[0]))

0.28071685840987737

X1, X2 = np.meshgrid(np.arange(0, 30, 0.5), np.arange(0, 30, 0.5))
Z = multivariate_gaussian(np.stack([X1.ravel(), X2.ravel()], axis=1), mu, var)
Z = Z.reshape(X1.shape)

plt.plot(X_train[:, 0], X_train[:, 1], 'bx')
plt.contour(X1, X2, Z, levels=10**(np.arange(-20., 1, 3)), linewidths=1)

plt.title("The Gaussian contours of the distribution fit to the dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.show()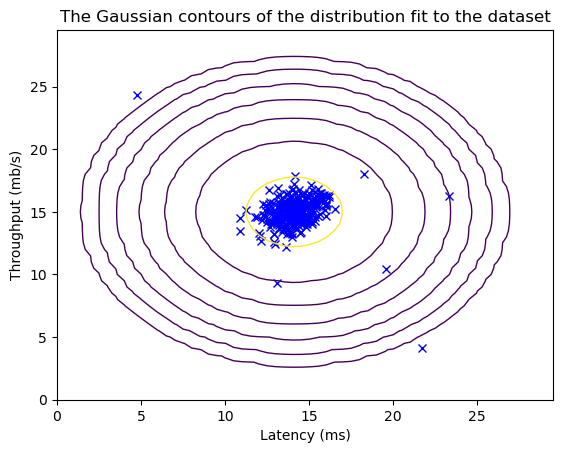

Selecting threshold $ϵ$

$$\begin{array}{rl}prec& =\frac{tp}{tp+fp}\\ rec& =\frac{tp}{tp+fn},\end{array}$$ $$F_1=\frac{2\cdot prec\cdot rec}{prec+rec}$$

def select_threshold(y_val, p_val):
    best_epsilon = 0
    best_F1 = 0
    F1 = 0

    step_size = (max(p_val) - min(p_val)) / 1000

    for epsilon in np.arange(min(p_val), max(p_val), step_size):

        predictions = (p_val < epsilon)

        tp = np.sum((predictions == 1) & (y_val == 1))
        fp = np.sum((predictions == 1) & (y_val == 0))
        fn = np.sum((predictions == 0) & (y_val == 1))

        prec, rec = 0, 0

        if (tp+fp) != 0:
            prec = (tp)/(tp+fp)
        if (tp+fn) != 0:
            rec = (tp)/(tp+fn)

        F1 = 0
        if (prec+rec) != 0:
            F1 = 2*prec*rec/(prec+rec)

        if F1 > best_F1:
            best_F1 = F1
            best_epsilon = epsilon

    return best_epsilon, best_F1

Finding Outliers

p = multivariate_gaussian(X_train, mu, var)
p_val = multivariate_gaussian(X_test, mu, var)
epsilon, F1 = select_threshold(y_test, p_val)

print('Best epsilon found using cross-validation: %e' % epsilon)
print('Best F1 on Cross Validation Set: %f' % F1)

Best epsilon found using cross-validation: 8.990853e-05
Best F1 on Cross Validation Set: 0.875000

outliers = p < epsilon

X1, X2 = np.meshgrid(np.arange(0, 30, 0.5), np.arange(0, 30, 0.5))
Z = multivariate_gaussian(np.stack([X1.ravel(), X2.ravel()], axis=1), mu, var)
Z = Z.reshape(X1.shape)

plt.plot(X_train[:, 0], X_train[:, 1], 'bx')
plt.contour(X1, X2, Z, levels=10**(np.arange(-20., 1, 3)), linewidths=1)
plt.plot(X_train[outliers, 0], X_train[outliers, 1], 'ro',
         markersize=10, markerfacecolor='none', markeredgewidth=2)

plt.title("The Gaussian contours of the distribution fit to the dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.show()

print('# Anomalies found: %d' % sum(p < epsilon))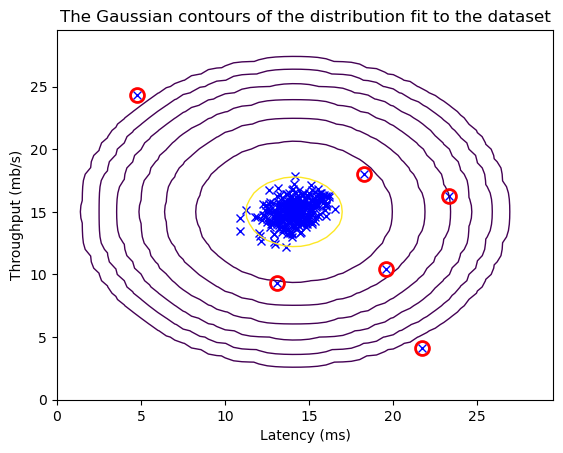

# Anomalies found: 6